绪言
废水处理的理论书中很少关注溶液的电导率计算过程,《给水排水设计手册》和《Wastewater Engineering》等经典教材也仅仅给出了总溶解性固体(TDS)和电导率之间的粗略关系(0.5~0.8,一般取0.6)。PHREEQC的作者C.A.J. Appelo博士提供了一种极为精妙的算法,特翻译以备研究交流之用。
正文
溶液的电导率(\(SC\),μS/cm)易于测量,非常适用于检查水模型的参数、确定新化学态的缔合常数。 PHREEQC根据带电型体的浓度与扩散系数来计算溶液的电导率,并采用离子强度进行修正。采用经典离子缔合模型与Pitzer模型得到的结果与大批量溶液的测量数据高度一致,这些溶液的电导率涵盖了从10到160,000 μS/cm的范围。下图比较了由P.J. Stuyfzand提供的数据与计算值。
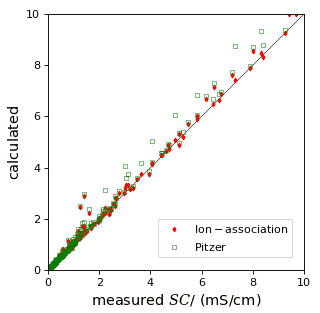
使用phreeqc.dat和pitzer.dat进行185次SC < 10000 μS/cm的分析,标准偏差分别为14和23 μS/cm。
一般而言,使用Pitzer计算的电导率略高。使用Pitzer的系数,可以在高盐度下很好地计算溶质的活度,但络合物通常就省略了(尽管从物理学上来说,它们可能是真实存在的)。与之相对,使用Debye-Hückel方法,为了获得高溶质浓度下正确的活度,通常必须包括络合物。这些络合物将阳离子和阴离子结合成一个电荷较小的实体,结果电导率降低。因此,络合物的稳定常数可以通过拟合简单溶液的电导率来获得,这导致电导率更逼近Debye-Hückel方法。但需要注意的是,在浓度大于1 M时,离子的摩尔电导率以一种尚不完全了解的方式变化。这带来的不确定性影响了混合物的计算,因此也影响了自然水体的\(SC\),特别是当\(SO_{4}^{2-} \)浓度较高时。
计算原理是不同型体的溶质的摩尔电导率和扩散系数之间存在如下关系:
\[ \Lambda_m^0=\frac{z^2F^2}{RT}D_w \]
\( \Lambda_m^0 \)是摩尔电导率(S/m /(mol/m3)),\( z \)是电荷数(无量纲),\( F \)是法拉第常数(C/mol),\( R \)是气体常数(J/K/mol),\( T \)是绝对温度(K),\( D_w \)是扩散系数(\( m^2/s) \)。将摩尔电导率乘以浓度\(m\)并对所有溶质求和,得到溶液的电导率的估算值:
\[ SC= \sum(\Lambda_m^0m) \]
唯一的问题是摩尔电导率随浓度变化。
科尔劳斯定律认为,等效电导率以浓度的平方根而降低:
\[ \Lambda_{eq}=\Lambda_{eq}^0-K(|z|m)^{0.5} \]
其中,\(K\)是科尔劳斯常数。我们可以使用\( \Lambda_{eq}(= \Lambda_m / |z|)) \)替\( \Lambda_m^0 \)来计算\( SC\)。或者,我们可以坚持使用\( \Lambda_m^0 \),但用电化学活性系数校正摩尔浓度。
当然,这两种方法应该产生相同的结果:
\[SC= \sum((\Lambda_{eq}^0-K(|z|m)^{0.5})|z|m)= \sum(\Lambda_m^0\gamma_{sc}m) \]
其中\( \gamma_{sc}\)是校正摩尔浓度或电迁移中的扩散系数的活度系数。
在3.3.9版本之前,PHREEQC,对于离子强度\(I < 0.36|z|\),Debye-Hückel活度系数的对数,是乘以0.6/\({|z|^{0.5}}\);其余情形采用\(I^{0.5} / |z| \)。
之后的版本使用:
\[ \gamma_{sc i}=exp(\frac{-a_{1i}A|z_i|\sqrt{I}}{1+\kappa a}), 其中,\kappa a=B\sqrt{I}\frac{a_{2i}}{1+I^{0.75}} \]
其中\(A\)和\(B\)是Debye-Hückel参数,\(a_1\)和\(a_2\)从二元盐溶液的测量的\(Cl^-\)传输数和电导率\(SC\)的数据中找到(Appelo,2017,Cem. Concr. Res. 101,102-113)。新方程对盐水更为适用。
PHREEQC的计算经过与《化学与物理手册》的数据核对,该手册列出了20°C时盐溶液的SC。
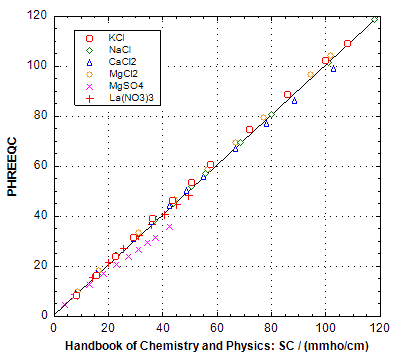
PHREEQC在输出文件中打印电导率\(SC\),而特殊的BASIC变量电导率SC将在关键字USER_PUNCH或_GRAPH中提供。使用PHREEQC输入文件salt_sc.phr计算的结果如上图所示。请注意,计算需要在PHREEQC.DAT和PITZER.DAT中的SOLUTION_SPECIES下给出的扩散系数。扩散系数通过以下公式校正到溶液的温度T(开尔文):
\[ (D_W)_T=(D_W)_{298}\times exp(d/T-d/298)\times(\eta_{298}/\eta_T) \]
其中d是一个系数,\(η\)是纯水的粘度。系数\(d\)、\(a_1\)和\(a_2\)通过SOLUTION_SPECIES中的-dw参数输入。
补充资料
计算步骤
根据上述文献的说明,总结推算溶液中电导率步骤如下:
(1)根据的离子型体的摩尔电导率、摩尔浓度和相应的活度系数计算电导率:
\[SC= \sum(\Lambda_m^0\gamma_{sc}m) \] Eq. (1)
(2)不同离子型体的摩尔电导率根据下式计算:
\[ \Lambda_m^0=\frac{z^2F^2}{RT}(D_w)_T \] Eq. (2)
(3)不同离子型体的活度系数根据下式计算:
\[ \gamma_{sc i}=exp(\frac{-a_{1i}A|z_i|\sqrt{I_m}}{1+\kappa a})\] Eq. (3)
(4)上式中的\(\kappa a\)
\[ \kappa a=(10^{10}\times\kappa)^{-1}\frac{a_{2i}}{1+I_m^{0.75}} \]Eq. (4)
(5)上式右侧括号内的\(\kappa\)按下式计算:
\[\kappa=\frac{1}{F}\sqrt{\frac{\varepsilon_wRT}{2\times 10^3 I_m}}\] Eq. (5)
(6)结合式(4)和(5),可知\(\kappa a\)
\[ \kappa a=\frac{F}{10^{10}} \sqrt { \frac{2 \times 10^3 I_m}{\varepsilon_w RT}}\frac{a_{2i}}{1+I_m^{0.75}} \] Eq. (6)
(7)不同离子型体在任意温度状态下的扩散系数与标准状态(298.15K)下的计算校正系数。
\[ (D_W)_T=(D_W)_{298}\times exp(d/T-d/298)\times(\eta_{298}/\eta_T) \] Eq. (7)
(8)式(3)、(4)、(5)、(6)中的离子强度\(I_m\)按侠士计算
\[ I_m=\frac{1}{2}\sum m_iz_i^2 \] Eq. (8)
变量表
上述计算中用到输入变量如下:
\(m_i\),不同离子型体的摩尔浓度,mol/m\(^3\)
\(T\),溶液温度,K
计算参数
其中不同离子的\(z\)、\(D_w\)、\(A\)、\(d\)、\(a_1\)和\(a_2\)等参数是上述计算的关键。
常量表
上述计算中用到常量如下:
\(F\),法拉第常数,96485.33289 C/mol
\(R\),气体常数,8.314 J/K/mol
\(\varepsilon_w\),水的介电常数,25℃下为\(6.94\times10^{-10} \) F/m
\(A\),Debye-Hückel参数,对于25℃的水溶液为0.510 (kg·mol\(^{-1}\))\(^{\frac12}\)
